선택정렬(selection sort)
선택정렬(selection sort)는 가장 작은 값부터 뽑아내어 정렬하는 방법입니다.
시간복잡도는 $O(N^2)$ 입니다.
init_list = [5, 12, 22, 35, 64, 53,72]
res_list = []
while init_list:
res_list.append(min(init_list))
init_list.pop(init_list.index(min(init_list)))
print(res_list)
삽입정렬(Insertion sort)
삽입정렬(Insertion sort)는 원소의 값이 들어갈 위치를 찾아 삽입해주는 방식입니다.
시간 복잡도는 최선일 경우 $O(N)$ , 최악의 경우 $O(N^2)$이 걸리는 방법입니다.
init_list = [5, 12, 22, 35, 64, 53,72]
res_list = []
def find_insertion_index(lst: list,val:int):
for i in range(len(lst)):
if lst[i] > val:
return i
return len(lst)
for i in init_list:
res_list.insert(find_insertion_index(res_list,i),i)
print(res_list)
병합정렬(merge sort)
병합정렬(merge sort)는 원소들을 분할 한 후, 하나 하나 정렬하여 병합하는 방식입니다.
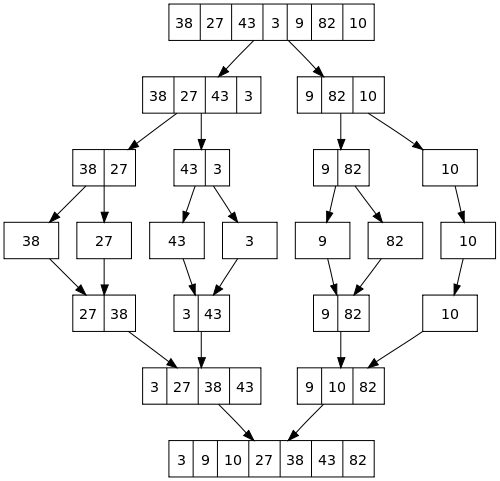
시간 복잡도는 최선/최악 모두 $O(N logN)$을 보여주는 상당히 빠른 정렬 방식입니다.
init_list = [5, 12, 22, 35, 64, 53,72]
def merge_sort(input_list: list):
length = len(input_list)
res = []
if length == 1:
return input_list
mid = length // 2
arr1 = merge_sort(input_list[:mid])
arr2 = merge_sort(input_list[mid:])
while arr1 and arr2:
if arr1[0] < arr2[0]:
res.append(arr1.pop(0))
else:
res.append(arr2.pop(0))
while arr1:
res.append(arr1.pop(0))
while arr2:
res.append(arr2.pop(0))
return res
print(merge_sort(init_list))
퀵정렬(quick sort)
퀵정렬은 pivot, 분할과정복 방식을 활용하여 정렬하는 방식입니다.
pivot을 기준으로 pivot보다 작은 값과 큰 값으로 분할하고, 이 분할된 원소들을 정렬하며 병합하는 방식입니다.
시간복잡도는 최선과 평균의 경우 $O(NlogN)$, 최악의 경우 $O(N^2)$ 입니다.
init_list = [5, 12, 22, 35, 64, 53,72]
def quick_sort(array: list):
if len(array) <= 1:
return array
pivot = array[0]
low_list = []
high_list = []
for i in array[1:]:
if i < pivot:
low_list.append(i)
else:
high_list.append(i)
return quick_sort(low_list) + [pivot] + quick_sort(high_list)
print(quick_sort(init_list))
*해당 글은 '제주코딩베이스캠프'님의 강의를 듣고 작성 되었습니다.
'알고리즘 > 이론' 카테고리의 다른 글
| [python] 플로이드 워셜(Floyd-Warshall) 알고리즘 (3) | 2022.09.29 |
|---|---|
| [python] 다익스트라(dijkstra) 알고리즘 (0) | 2022.09.27 |
| [python] BFS (0) | 2022.09.26 |
| [python] DFS (1) | 2022.09.23 |
| [python] 이진 탐색(Binary Search) (0) | 2022.09.22 |